Workshop on the occasion of Prof. Alexander Iksanov’s 50th birthday
Synopsis
The workshop will be held online on May 24, 2022. It is dedicated to the 50th anniversary of Prof. Alexander Iksanov and aims to bring together his collaborators and friends from various fields of probability theory and deliver short lectures reflecting his scientific interests.
Short Bio

Alexander Iksanov was born on March 17, 1972 in Kyiv. He graduated in 1995 from the Faculty of Cybernetics of Taras Shevchenko National University of Kyiv. Since then his scientific carrier is inextricably linked with the Alma Mater. In 2000 he defended his PhD thesis under the supervision of Prof. Oleg Zakusylo and in 2007 he defended his habilitation “Fixed points of inhomogeneous smoothing transformations”. Since 2008 he is a professor at the Department of Operations Research of the Faculty of Cybernetics. Starting from January 16, 2014 and till now he holds the position of the Head of the Operations Research Department. The scientific interests of Prof. Iksanov are broad and included at various stages:
- (AX+B)-Markov chains and perpetuities;
- branching random walks and other branching processes;
- exchangeable coalescents;
- fixed points of smoothing transforms;
- infinite occupancy schemes and infinite occupancy schemes in random environment;
- shot noise processes and random processes with immigration;
- regenerative compositions and partition structures;
- renewal theory and its applications;
- standard random walks, perturbed random walks and random walks with a barrier;
- topics in probabilistic number theory.
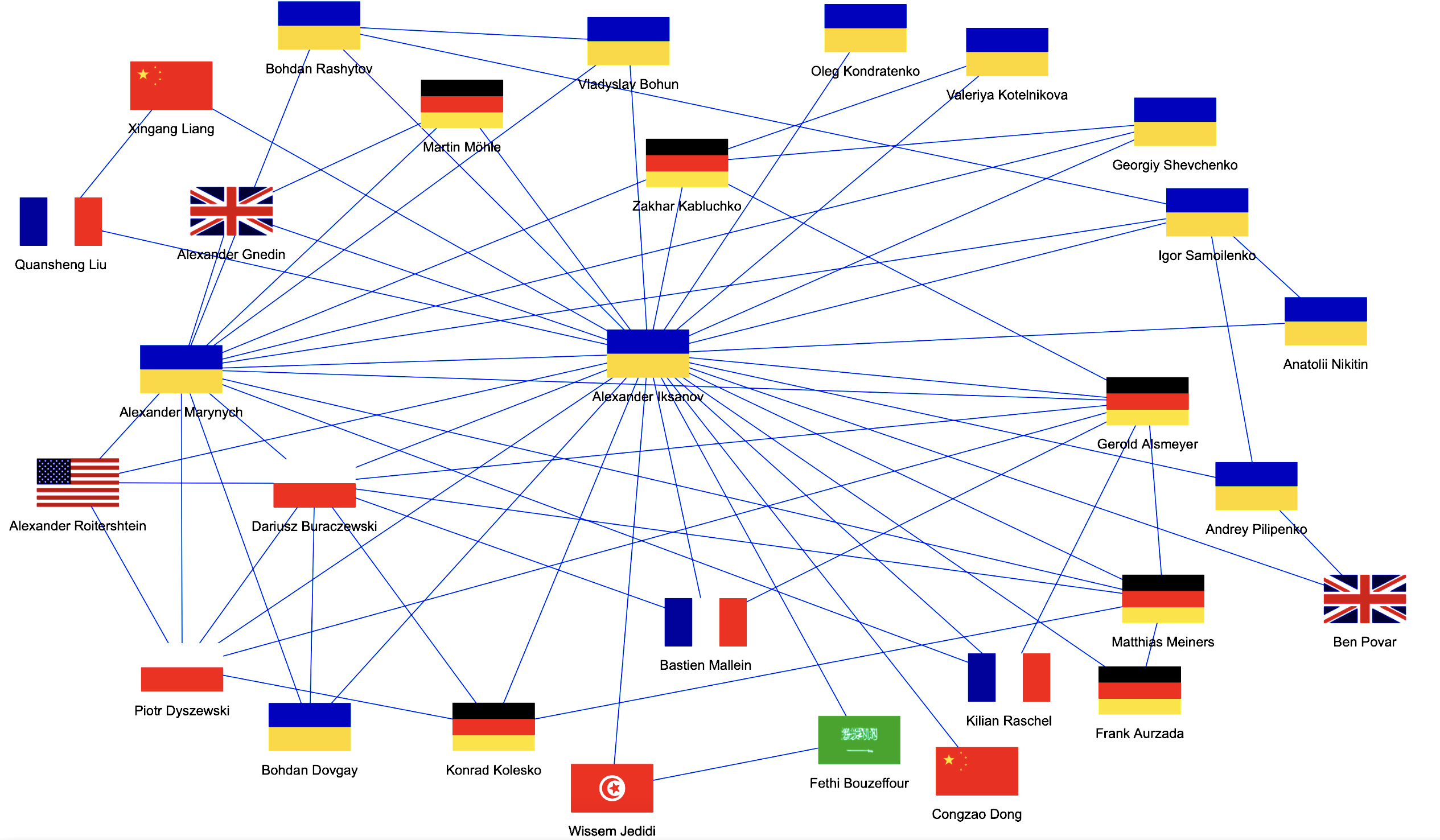
Prof. Iksanov enjoys a wide collaboration network all over Europe, in particular, he maintains close contacts with probabilists in France, Germany, Poland and the UK.
Collaboration network of Alexander Iksanov for the last 10 years (according to ArXiV.org). Graphics by B. Mallein and A. Marynych.
Participants
- Gerold Alsmeyer (Münster, Germany)
- Vladyslav Bohun (Kyiv, Ukraine)
- Dariusz Buraczewski (Wrocław, Poland)
- Oksana Braganetz (Kyiv, Ukraine)
- Ewa Damek (Wrocław, Poland)
- Bohdan Dovgay (Kyiv, Ukraine)
- Alexander Iksanov (Kyiv, Ukraine)
- Andriy Ilienko (Kyiv, Ukraine)
- Zbigniew Jurek (Wroclaw, Poland)
- Alexander Gnedin (London, UK)
- Zakhar Kabluchko (Münster, Germany)
- Konrad Kolesko (Gießen, Germany)
- Valeriya Kotelnikova (Kyiv, Ukraine)
- Bastien Mallein (Paris, France)
- Alexander Marynych (Kyiv, Ukraine)
- Matthias Meiners (Gießen, Germany)
- Viacheslav Melnykov (Kyiv, Ukraine)
- Martin Möhle (Tübingen, Germany)
- Anatoliy Nikitin (Ostroh, Ukraine)
- Andriy Pilipenko (Kyiv, Ukraine)
- Kilian Raschel (Angers, France)
- Bohdan Rashytov (Kyiv, Ukraine)
- Uwe Rösler (Kiel, Germany)
- Ihor Samoilenko (Kyiv, Ukraine)
- Oleg Zakusylo (Kyiv, Ukraine)
- Andriy Zavorotynskiy (Kyiv, Ukraine)
Schedule
Time zone is CET!
| Speaker | Title / Abstract | Time |
|---|---|---|
| Oleg Zakusylo | Foreword | 13:40 – 13:50 |
| Gerold Alsmeyer | Recurrence/transience of random affine recursions in the divergent contractive and the critical case
I will speak about some recent results obtained together with Sasha and Dariusz Buraczewski about the recurrence/transience of random affine recursions Xn=MnXn-1+Qn, n=1,2,… for i.i.d. R+2-valued (M1,Q1), (M2,Q2),… in cases when the Goldie-Maller conditions for positive recurrence fail to hold. This amounts to a discussion of the critical case when the random walk Sn=log(M1)+log(M2)+…+log(Mn) is oscillating, and the divergent contractive case when Sn → -∞ a.s. (negative divergence), but positive recurrence of (Xn)n≥0 fails to hold. |
13:50 – 14:20 |
| Dariusz Buraczewski | Random walks in a strongly sparse random environment
The integer points of the real line are marked by the positions of a standard random walk with positive integer jumps. We assume that the set of marked sites is strongly sparse, i.e. the jumps of the random walk have infinite mean and regularly varying. We consider a nearest neighbor random walk on the set of integers having jumps +/-1 with probability 1/2 at every nonmarked site, whereas a random drift is imposed at every marked site. We will present some new limit theorems for the so defined random walk in a strongly sparse random environment. The talk will be based on a joint work with Alexander Iksanov, Piotr Dyszewski and Alexander Marynych. |
14:20 – 14:50 |
| Matthias Meiners | Fluctuations of martingales in branching processes
A recurring theme of my joint work with Alexander is the fluctuations of martingales in branching processes. I will give a brief overview of our joint works in this area. |
14:50 – 15:20 |
| Bastien Mallein | Derivative martingale of the branching random walk
A branching random walk is a population model on the real line in which each particle moves and creates offspring around its location in an independent manner. This system invades its environment at a linear growth rate, with a random delay that can be expressed in terms of the limit of the so-called derivative martingale. In this talk, we will study the right tail of this random variable by characterizing the sub-harmonic functions of the killed random walk with linear growth. This is based on a joint work with Dariusz Buraczewski and Alexander Iksanov. |
15:20 – 15:50 |
|
40-minutes break |
||
| Zakhar Kabluchko | Limit theorems for profiles of random trees
In this talk we shall review limit theorems for profiles of binary search trees and random recursive trees. A simple inductive way to generate a random recursive tree is as follows. At time 1 we start with a tree consisting of a single vertex (the root) labeled with 1. At each time k, given a recursive tree with k vertices, we choose one of the k vertices uniformly at random and add to this vertex an offspring labeled with k+1. The random tree obtained at time n is called the random recursive tree with n vertices. We are interested in the profile of the random recursive tree, which is the function k→Ln(k) counting the number of vertices at distance k from the root in a tree with n vertices. We shall review distributional and functional limit theorems for the random variables Ln(k) as n→∞ and k=k(n) is some function of n (which may stay constant or go to ∞ at some speed). The talk is based on joint works with A. Iksanov, A. Marynych and H. Sulzbach. |
16:30 – 17:00 |
| Martin Möhle | On a particular coupling and its applications to random trees
A particular coupling related to a random walk allows to derive a weak convergence result for the number of cuts needed to isolate the root of a random recusive tree. This result has direct consequences for the number of collisions that take place in the Bolthausen-Sznitman coalescent until there is just a single block. The coupling turns out to be useful to derive the asymptotics of the absorption time of certain Markov chains, in particular the number of collisions in beta(a,1)-coalescents with parameter 0 < a < 2. Generalizations are briefly discussed. The talk is based on a cute joint work with Alexander Iksanov published in 2007. |
17:00 – 17:30 |
| Alexander Gnedin | Renewal and regeneration in combinatorics
Many classic combinatorial structures are decomposable in component elements called blocks. A random structure is regenerative if removing in some way a block yields a reduced structure similar to the whole. This general idea has been realised in terms of exchangeable partitions and their ordered counterparts, and connected to continuous time/space processes. The talk is devoted to Sasha Iksanov’s fundamental contribution to the analysis of this connection and |
17:30 – 18:00 |
| Alexander Marynych | Renewing the renewal theory
If one aims to single out the most important unifying ingredient of our hero-of-the-day’s works, the most accurate answer should be “(highly advanced) renewal theory”! In this speech I will provide numerous evidences to this statement and bring together under a single umbrella all the previous talks. |
18:00 – 18:30 |